2024-12-27
Learning Solver Design: Automating Factorio Balancers
I find declarative programming fascinating: we just model the problem, describe the result we want, and an “oracle” (a.k.a. solver) conjures a solution for us. A lot of smart people spent decades building solvers for different problem classes, and I wanted an excuse to go and play with some of these solvers to learn optimization tricks along the way.
In this post, I describe what I learned solving a toy flow optimization problem with MIP and SAT solvers. I picked belt balancing from the Factorio video game. It looks innocuous at first, but it's in reality NP complexity. It's possible to solve by hand small versions, allowing us to check correctness, but it quickly becomes impossible to humanly solve even for medium size balancers that are very useful in the game. What the majority of players do is use pre-built online solutions. The game incentivizes sharing designs, called blueprints, as a string, and there's a thriving community that comes up with clever solutions.
Let's define the problem next.
The Throughput-Unlimited Factorio Belt Balancer
A core dynamic in Factorio is transporting items between different production buildings using conveyor belts, e.g., transporting raw stone from a mining drill to a Stone Furnace to be transformed into a brick. Since the throughput of a belt lane is limited, it's necessary to have multiple parallel lanes. To help prevent bottlenecks in the factory, parallel lanes need to be balanced, for example, a slow miner from slowing down producing steel plates.
The last Furnace is sometimes idle waiting for new resources. We don't want that.To perfectly balance two belt lanes, we can use a Mixer component: that's a 2x2 Belt Balancer. There's an issue that arises with more than two lanes: the output flow may be lower than the input, slowing down all the lanes. We want two properties: all the inputs need to be connected to all the outputs, and the total maximum flow in input needs to be maintained in output. If only the former problem is solved, we have a Throughput-Limited balancer, which is easier to build, takes up less space, but unfortunately slows down all the lanes. The Throughput-Unlimited Belt Balancer instead ensures that every input flow is evenly distributed across all the outputs.
Example of 4 x 4 naïve Throughput-Limited belt balancer. This is not what we want.Given the exponential complexity, we cannot expect to find arbitrarily large solutions, but my approach works well in practice since rarely players use larger than 16x16 balancers. For this project, I focused on finding a reasonably small feasible balancers, prioritizing small 2D area occupied, without necessarily finding the optimal number of components.
4 x 4 Throughput-Unlimited belt balancer. This is what we want.As a first implementation, we model the problem as Mixed Integer Programming (MIP).
Continuous flows: Mixed Integer Programming
This first model is Mixed Integer Programming, we use the SCIP solver and Google OR-tools framework. Input flows are modeled as separate float variables. Every input flow should be present in every output in equal measure. I created a binary variable array for every component and every direction on every 2D cell in the grid. We have three types of components: belts, underground belts, and mixers. Belts take up one cell, mixers take up two cells, and underground belts take up two cells. Underground belts are set apart up to a maximum distance, modeled as an extra dimension on the array e.g. entrance 3 cells away is u[x][y][d][3] where x, y are the coordinates of the cell that contains the entrance, d is the direction and 3 is the distance of the exit in direction d from the entrance.
After modeling all the rules as constraints, this first implementation solves immediately small grids, for example, it can compute a 2x2 balancer and transport multiple parallel flows to the other side of the grid, both trivial problems, but it gives us confidence that the constraints are implemented correctly. The main problem of this approach is numeric instability: since the flows are modeled as floating point variables and there are a lot of equality constraints, on a 3x3 balancer the numeric errors accumulate and make it very hard to converge on a solution.
Since this model doesn't even scale to a 3x3 balancer, I needed to explore alternative approaches. Before migrating to a different solver, let's build tests and tooling to inspect the solution.
How to test the solution
Firstly, we need to represent the output in the console to quickly see if it's correct. We represent every component with a Unicode character: ▲ for belt, ↿↾ for mixer, and ▷‧‧‧↦ for underground belt at distance 3.
Secondly, we build tests around very simple cases:
- transport a single flow on the opposite side of the grid
- mix two flows with a single mixer
- use underground belts to minimize the number of components used. Maintaining tests gives us confidence that every change we'll make won't break previous solutions.
It proved to be very valuable to also represent flows entering and exiting every cell according to the rule of the components. Many times I modeled the constraints slightly incorrectly and the solver cleverly exploited bugs in my model to quickly reach a simple but incorrect solution.
Another very useful tool is testing the solution inside the game. Factorio conveniently accepts a base64 representation of the components on the 2D grid, so we can easily validate that the solution found works correctly.
Lastly, a powerful debugging technique I invented to spot broken constraints is providing a known solution and see what constraints it violates. If a constraint is violated, it needs to be fixed in order to make the solution pass without breaking the tests.
With all these new fancy tools, we can simplify the model by migrating to CP-SAT.
Discretize flows: CP-SAT
CP-SAT is a Satisfiability solver built at Google. It can't deal with floating variables, so we have to discretize the flows. It solves the numeric instability problem, but it raises a new issue: needing to know in advance how many times the input flows will be split before reaching the output. Usually, it's necessary to set the input flow to at least a multiple of 2^number_of_splits to ensure the split can always be represented by an integer.
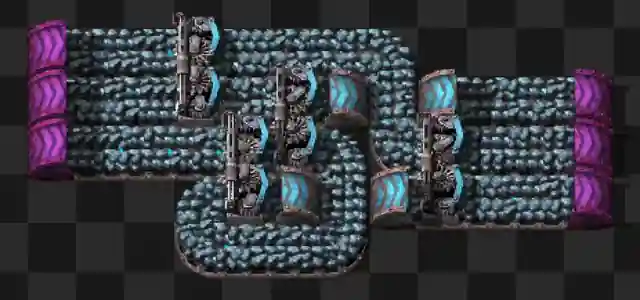3 x 3 belt balancerBesides changing the flow variables type, nothing else in the model needs to be changed and yields solutions up to 6x6 balancer in very little time. We find an 8x8 after 30min of computation, suggesting an excessive number of free binary variables in the model and a very large search space.
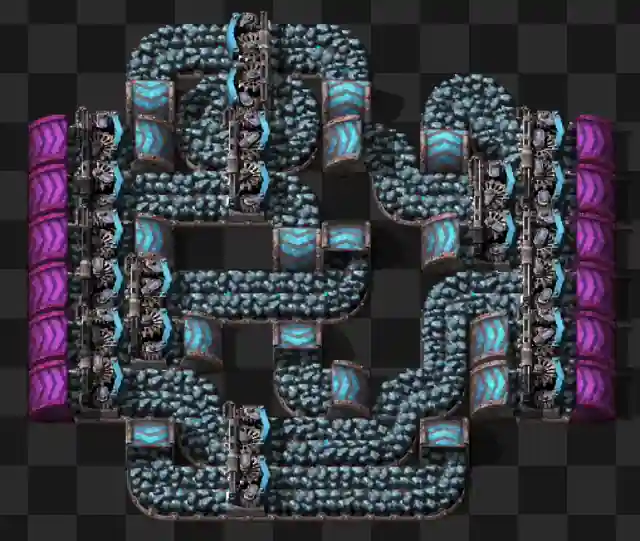6 x 6 belt balancer
8 x 8 belt balancerNext, we can represent underground belts as two independent components, rather than an extra dimension in the belt array. We can model the underground flow with a second flow grid, that interacts with the rest of the flow through underground belt components.
We can also provide hints to the solver that the underground flow is zero in most cases. I don't know exactly why it works, but a plausible explanation is that zeroing underground flow implies not using underground belts, and since they are very sparse in known solutions it converges faster.
Additionally, if we assume that the first and the last rows must have mixers and we add a couple of belt components at random, applying a technique called symmetry breaking, the solver finds an 8x8 solution in just 83s, a great improvement!
After spending a few hours changing the problem formulation, objective function, using hints, and solver strategies, I eventually hit a wall trying and I was never able to find a 16x16 balancer. The next trick in the book is decomposing into sub-problems that could be solved independently, let's see how.
Pre-computing flow between mixers with Banes Networks
Trying to model some balancers by hand, I noticed a common layer structure. In the first layer, two sources are mixed together, in the second, two mixed flows from the first layer are mixed with other two, etc. This suggests that I can abstract how flows are mixed and provide it to the solver as an additional constraint. Then the solver only needs to decide where to place a pre-computed number of mixers and how to connect them using belts. We can also lower the cardinality of the flows since we don't have to guarantee maximum throughput explicitly.
In order to force the output of a mixer to go as input of the next one, I made them different flows reducing to a graph coloring problem. Empirically, I observed that the number of different flows (edge colors in the graph) grows linearly with the number of inputs and outputs.
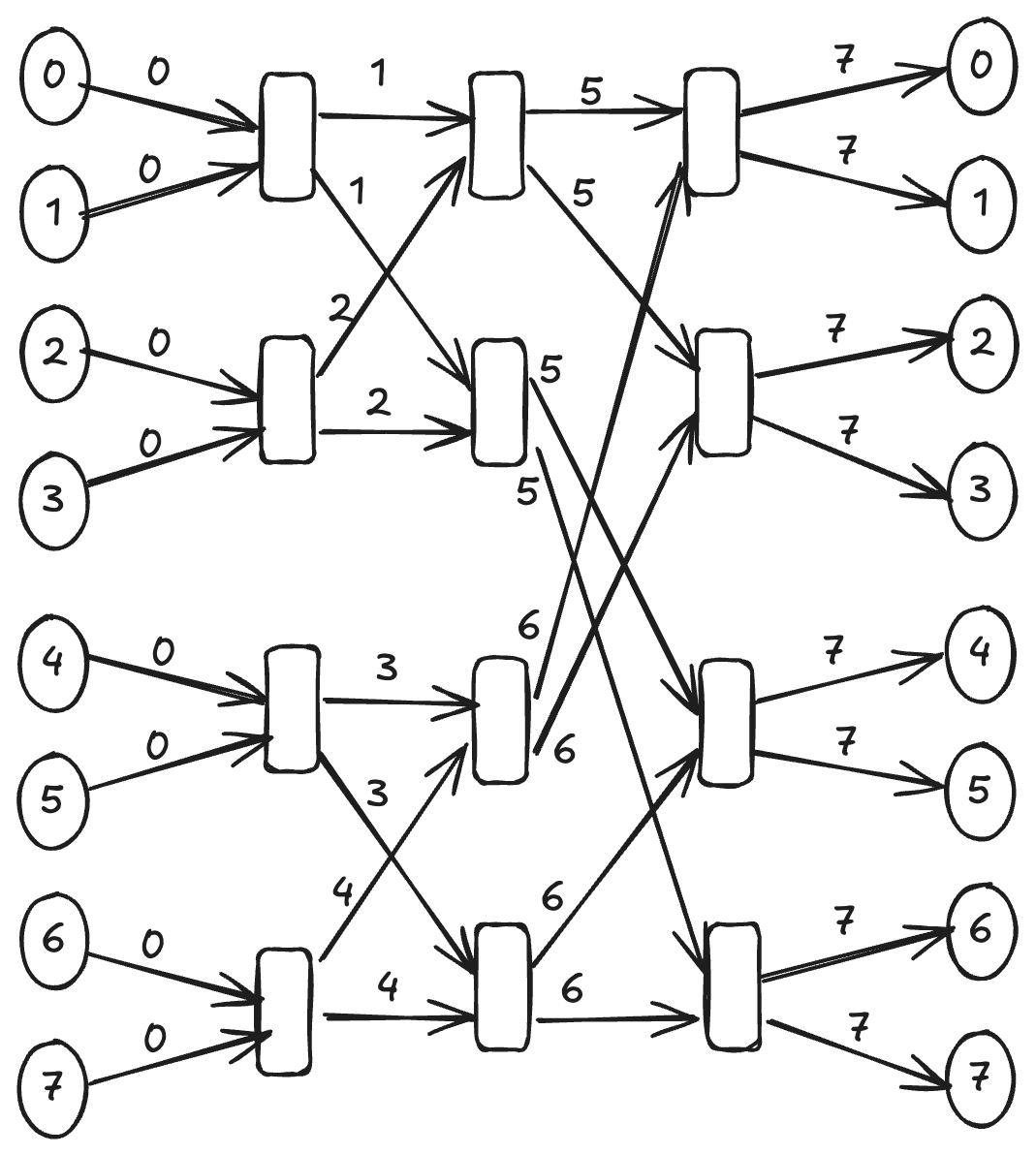Banes network for an 8x8 balancerI found out that these abstract flow networks with two inputs and two outputs are called Banes networks, they are a special case of Clos Networks.
They are very easy to build by hand since they follow a regular structure, so we can skip designing a greedy algorithm to build them for now and simply hard-code them as input.
This change alone wasn't able to produce a solution for a 16x16 balancer because the program kept getting killed due to high memory consumption. Let's see next how to trade a lower memory footprint for a higher running time.
Reduce the number of binary variables
One last optimization we can make is lowering the number of binary decision variables to reduce the solution search space. We can consolidate the direction of components: rather than having one more dimension in every component type array, we can have a separate array with the four dimensions.
The direction variable dc can be combined with the other variables (e.g. the belts variable b) to enforce the constraints only if they are both True.
The optimization reduces component decision variables by roughly 50%, drastically cutting the amount of memory needed. Here you can see 31K boolean variables before the optimization.
After the optimization we're left with only 12K. We effectively traded fewer variables (less memory) for more constraints (more CPU time spent verifying every candidate solution).
This technique, combined with placing mixers on first and last rows and symmetry breaking, allows us to find the solution of the 16x16 balancer in about 55min.
16 x 16 belt balancer
I'm pretty satisfied with the result and I decided to stop here since finding a 32x32 is exponentially harder and will require many more optimizations.
A curious bug
While testing a balancer in-game, I realized it was producing less than the maximum theoretical throughput on some outputs. That was due to a belt not curving as a consequence of an adjacent straight belt. This condition happens only if we're merging flows from two belts without using a mixer, a condition that should never happen in practice.
16 x 16 belt balancer with a bottleneck due to an implicit constraint.
After some debugging, I realized that it's due to the solver stopping when it finds the first feasible solution, without trying to remove unnecessary components and leaving extra belts around where it should leave empty spaces. The solution is simple: add an objective function that penalizes solutions using more components. Finding a slightly more optimal solution than the first feasible one is trivial and doesn't take the solver much time. Counterintuitively, adding an objective function brought down the time for solving a 16x16 to 30min, likely because having an objective skews the solver towards a feasible solution faster than random search.
Conclusions
We started this journey building a linear model with continuous variables and having SCIP finding very simple solutions, but could not even crack a 4x4 balancer that is easy to build by hand. Migrating to CP-SAT and applying various optimizations allowed us to obtain an 8x8 balancer that is definitely very hard to build by hand. Splitting the problems in two sub-problems: pre-computing mixer wiring with Banes Networks and placement with CP-SAT allowed us to scale and find the exponentially harder 16x16 balancer that I can confidently say it's impossible to find by hand.
Here's the table of CPU time needed (measured with the time command) to find a solution on my 12 cores Macbook Pro M4:
Balancer | MIP SCIP | CP-SAT | CP-SAT Banes Networks | CP-SAT Banes Networks memory optimized |
2x2 | 0.06s | 4.94s | 0.17s | 0.19s |
3x3 | -- (Never terminating after few hours) | 22.34s | 22s | 23s |
4x4 | -- | 25.50s | 22s | 19s |
6x6 | -- | -- | 2583s | 2399s |
8x8 | -- | 5669.16s | 1365s | 2168s |
16x16 | -- | -- (Requires too much memory) | -- (Requires too much memory) | 19173s (heuristic initial mixers placement and symmetry breaking) |
It's been an interesting journey and you can find all the code here. We learned how to model for SCIP and CP-SAT solvers. We used both linear and non-linear constraints. We observed how small changes to the model wildly change the solving time. We made a memory/CPU tradeoff to find the 16x16 balancer. And lastly we've seen the role of the objective function in finding a valid solution that works well in practice without having to add additional explicit constraints.